今天要來講解隨機森林Random Forests，接續上一節所講解的決策樹Decision Trees，並且有提到說Random forest是建立在決策樹上的學習集合。在前一節有提到，決策樹經常會遇到擬合的問題，而在隨機森林演算法中，因為forest是由多個Trees所組成，所以對隨機森林反而希望計算速度快速為要點，不會追求單顆tree擬和的情形。所以，會以Ensembles of Estimators- Random Forests講解為何不需要太在意Trees的擬合狀況。

• Ensembles of Estimators: Random Forests
  可以組合多個過度擬合估計器以減少過度擬合對 forest的影響 ，在SKlearn中的BaggingClassifier利用平行估計器的集合，將每個估計器都過度擬合數據，對數據求平均值以找到更好的分類。

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

tree = DecisionTreeClassifier()
#通過每個估計器擬合80％的訓練點
bag = BaggingClassifier(tree, n_estimators=100, max_samples=0.8,
                        random_state=1)

bag.fit(X, y)
visualize_classifier(bag, X, y)

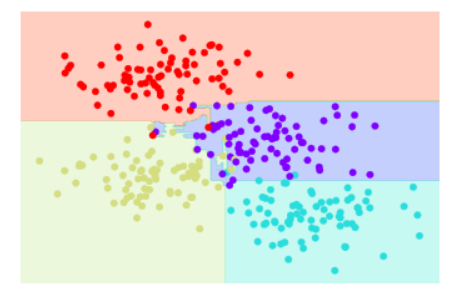
隨機森林主要應用模組：RandomForestClassifier

from sklearn.ensemble import RandomForestClassifier

model = RandomForestClassifier(n_estimators=100, random_state=0)
visualize_classifier(model, X, y);

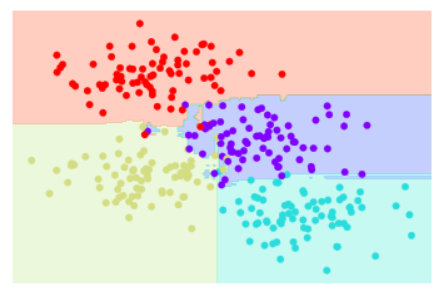
可以在上圖看到，他對資料的分割更加正確。

Random Forest Regression

將隨機森林結合之前講解的線性回歸，將資料回歸至一條線上，並進行預測。使用sin()正弦函數，可以看到輸出結果的圖形，符合正弦函數的圖型。

rng = np.random.RandomState(42)
x = 10 * rng.rand(200)

def model(x, sigma=0.3):
    fast_oscillation = np.sin(5 * x)
    slow_oscillation = np.sin(0.5 * x)
    noise = sigma * rng.randn(len(x))

    return slow_oscillation + fast_oscillation + noise

y = model(x)
plt.errorbar(x, y, 0.3, fmt='o');

• 再來直接利用SKlearn中的RandomForestRegressor，來繪製出回歸線

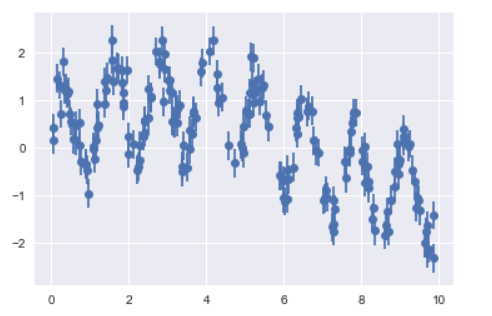
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(200)
forest.fit(x[:, None], y)

xfit = np.linspace(0, 10, 1000)
yfit = forest.predict(xfit[:, None])
ytrue = model(xfit, sigma=0)

plt.errorbar(x, y, 0.3, fmt='o', alpha=0.5)
plt.plot(xfit, yfit, '-r');
plt.plot(xfit, ytrue, '-k', alpha=0.5);

• 以sklearn中的手寫數字集合來舉例：

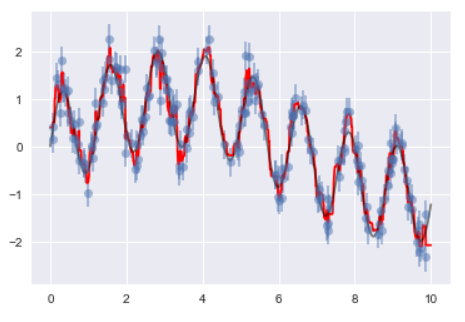
from sklearn.datasets import load_digits
digits = load_digits()
digits.keys(

可以看到上圖，資料keys包含'data', 'target', 'target_names', 'images', 'DESCR'

• 將手寫的資料視覺化呈現，可以看到每個數字(images)的左下角會記錄該數字的正確值(target)

# set up the figure
fig = plt.figure(figsize=(6, 6))  # figure size in inches
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

# plot the digits: each image is 8x8 pixels
for i in range(64):
    tx = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
    tx.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest')
    
    # label the image with the target value
    tx.text(0, 7, str(digits.target[i]))

• 將手寫資料分test、train資料，並利用上面介紹RandomForestClassifier()的方法將手寫數字進行分類。

from sklearn.cross_validation import train_test_split
from sklearn import metrics

Xtrain, Xtest, ytrain, ytest = train_test_split(digits.data, digits.target,
                                                random_state=0)
model = RandomForestClassifier(n_estimators=1000)
model.fit(Xtrain, ytrain)
ypred = model.predict(Xtest)

print(metrics.classification_report(ypred, ytest))

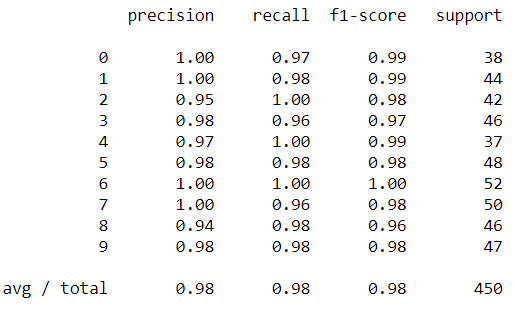
可以看到上圖，最左邊為數字0~9的類別，主要回傳精確值以及support，看這些數字很難懂，先看下圖

from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, ypred)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False)
plt.xlabel('true label')
plt.ylabel('predicted label');

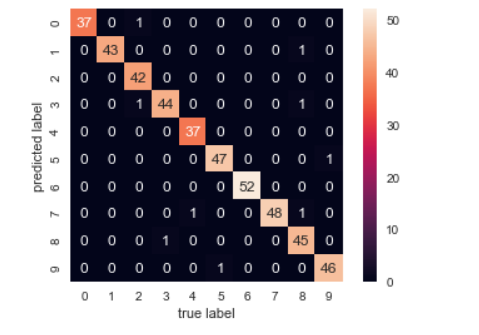
可以看到上圖，X軸為真實手寫數字的值，Y軸會預測手寫的數字的值，其斜對角0對0、1對1、2對2...，代表預測的準確次數(對照前一輸出結果的support)，將該類別準確次數/全部筆數=精確值(對照前一輸出結果的precision)